Day 14: Number Systems
CMSC 201 Day 14: Number Systems
Agenda:
Goal: Learn about files, maybe have fun :)
Your typical lecturer's email is: sdonahue@umbc.edu (Shane Donahue), no office hours this week :( You can still email me or your TA with questions.
Intro
Hello! I/we am/are your guest lecturer(s) :)
Project #1
Project #1 is still out! It's due Friday 2024-11-01 (Nov 1) at 11:59:59 PM! (So you have this week remaining.)
HW6 (recursion) will be released this Friday.
Alien counting
Aliens have landed on Earth!!! 😱😱😱 They are amorphous blobs with distinctly three fingers per "hand".
Foremost alien experts are attempting to initiate conversation with the mothership. But we're left to wonder... how do they count things?
Human counting is based on us typically having 10 fingers.
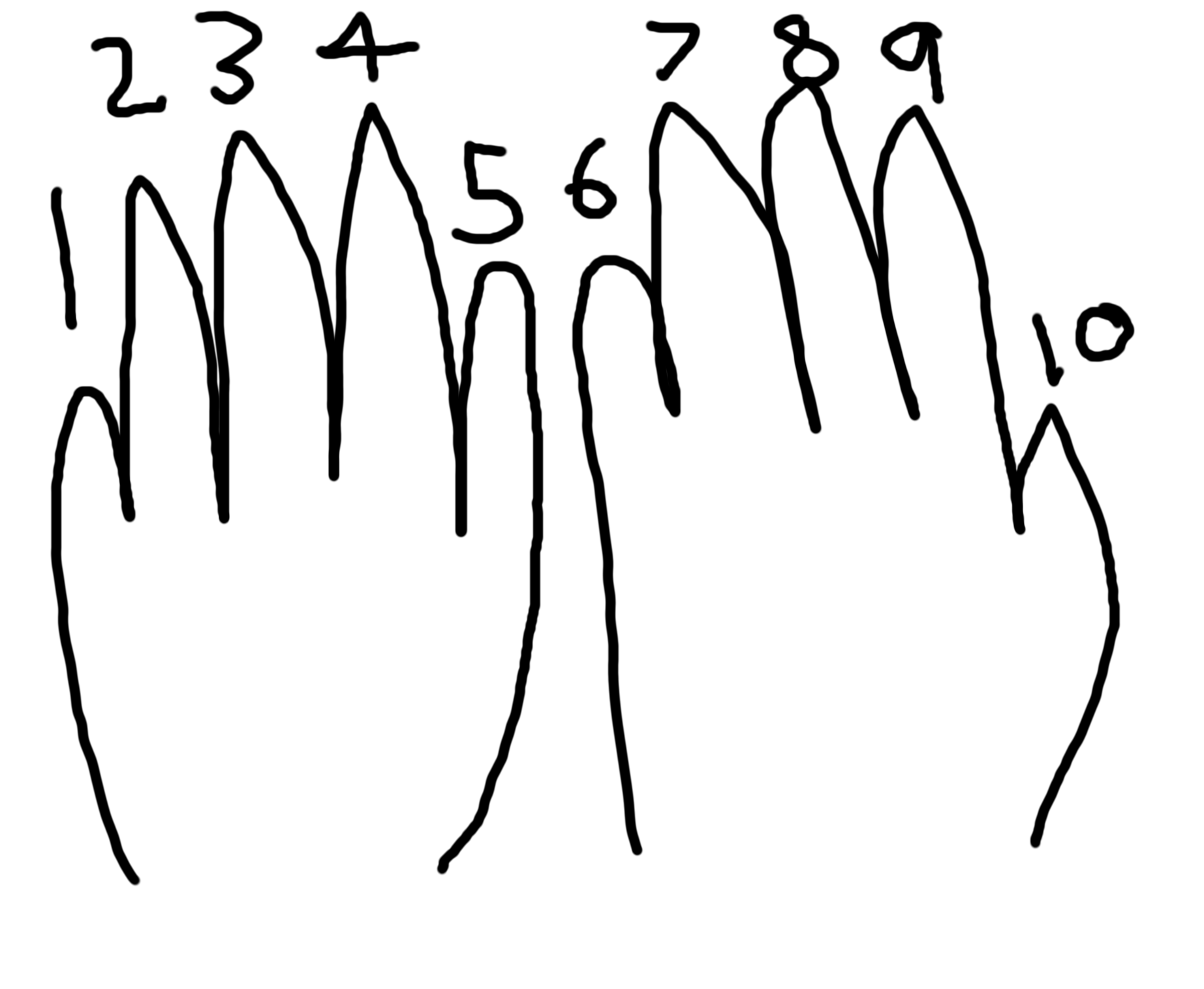
What happens for them?
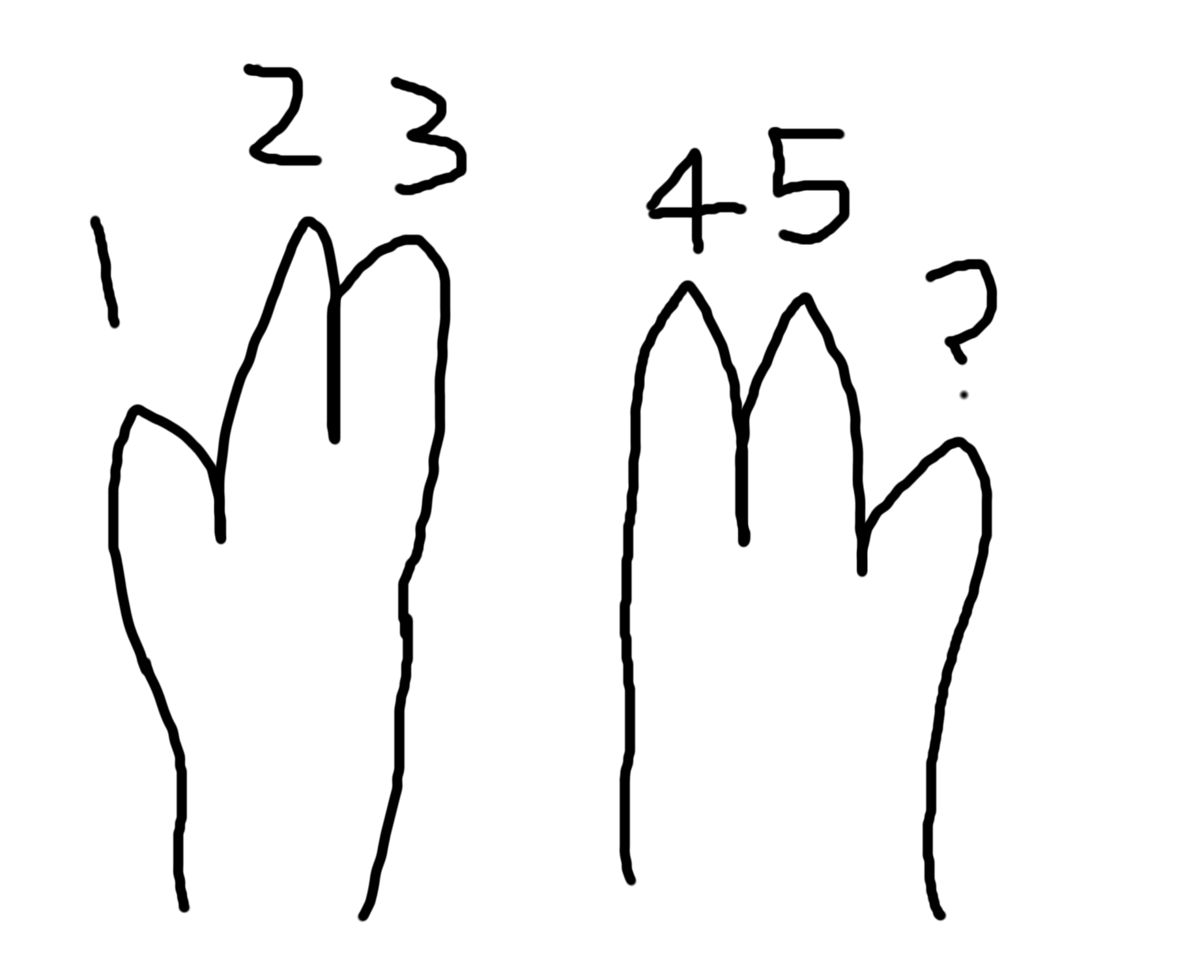
1, 2, 3, 4, 5... what next? Six does not exist for these aliens!
Much like when humans run out of numbers (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), they wrap around and use the same numbers again!
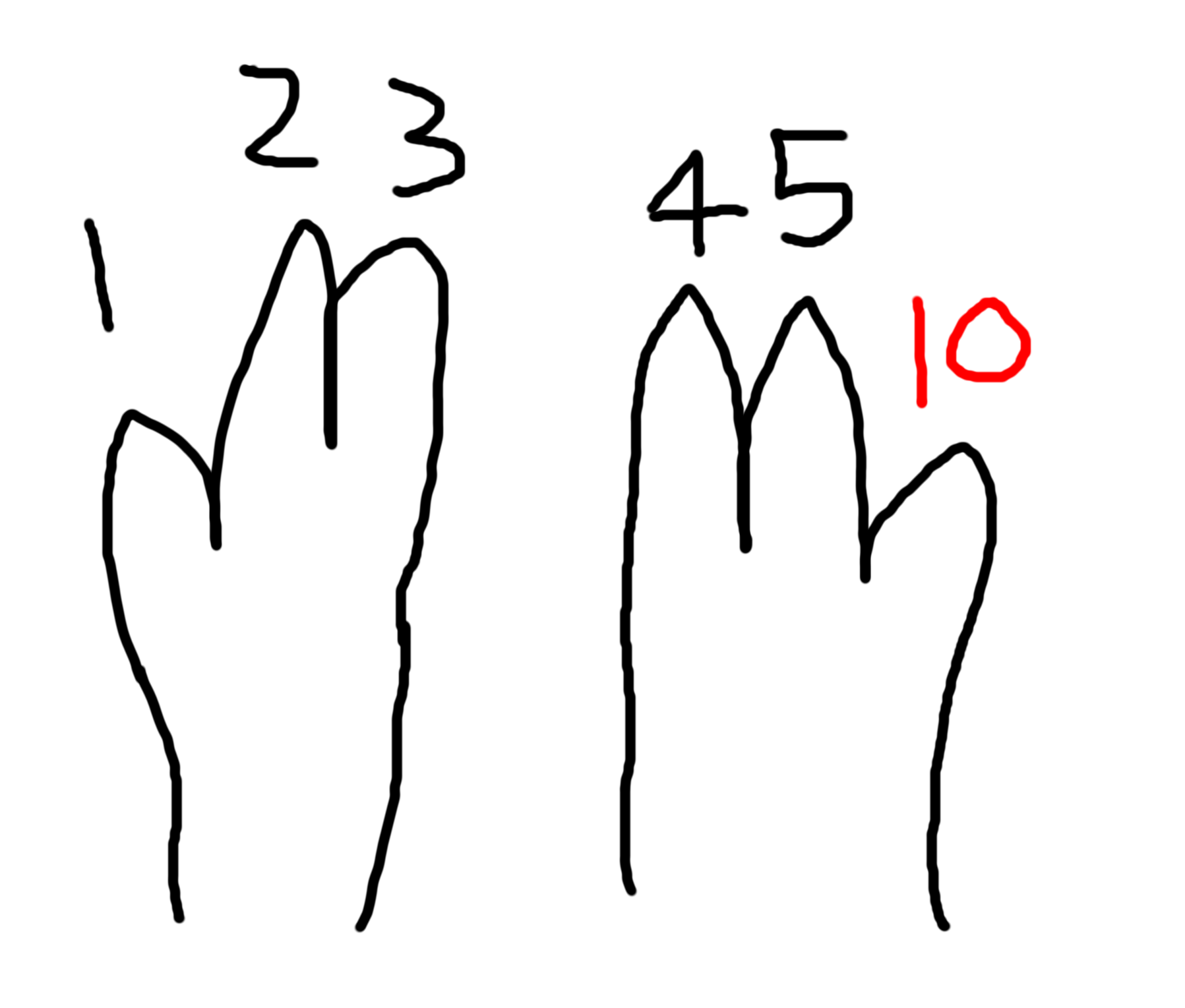
What? Isn't that just 10? Well yes, but it's 10 in a different base. Here's a comparison:
| Human counting | Alien counting |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 10 |
| 7 | 11 |
| 8 | 12 |
| 9 | 13 |
| 10 | 14 |
| 11 | 15 |
Alien "10" is human counting "6". That's confusing! How can we talk about these numbers in the correct contexts?
In this alien counting scheme, there are six unique values: 0, 1, 2, 3, 4, 5. So we call this base six.
In human counting, there are ten unique values, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, so we call this base ten or decimal. The names of the bases are themselves in decimal... :)
So, just like in the table, 10 (base 6) == 6 (base 10). 11 (base 10) == 15 (base 6). Another way of writing this is with subscripts. So, 106 == 610.
With one number, humans (decimal) can represent ten unique values. With one number, these aliens (base six) can represent six unique values.
How many values can humans represent with two numbers (two digits)? that would be 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13... until 99. That's 100 unique values! (We include 0 as a unique value). What about with three digits? That's 0 through 999, or 1000 unique values! Do you see a pattern?
Number of unique values == basenumber of digits. Three decimal digits == 103 == 1000. So, 20 decimal digits can represent 1020 possible values.
What about the aliens? How many values can the aliens represent with one digit? Six. How many can they represent with two digits?...
62 == 36 unique values! What about 10 digits? 10 alien digits can represent 610 unique values.
Binary and hexadecimal
Oh no! Our counting has been interrupted. Another set of aliens have arrived. They have eight fingers!

How do they count?!
One option is to just make up new symbols. How about zero through nine, then letters?
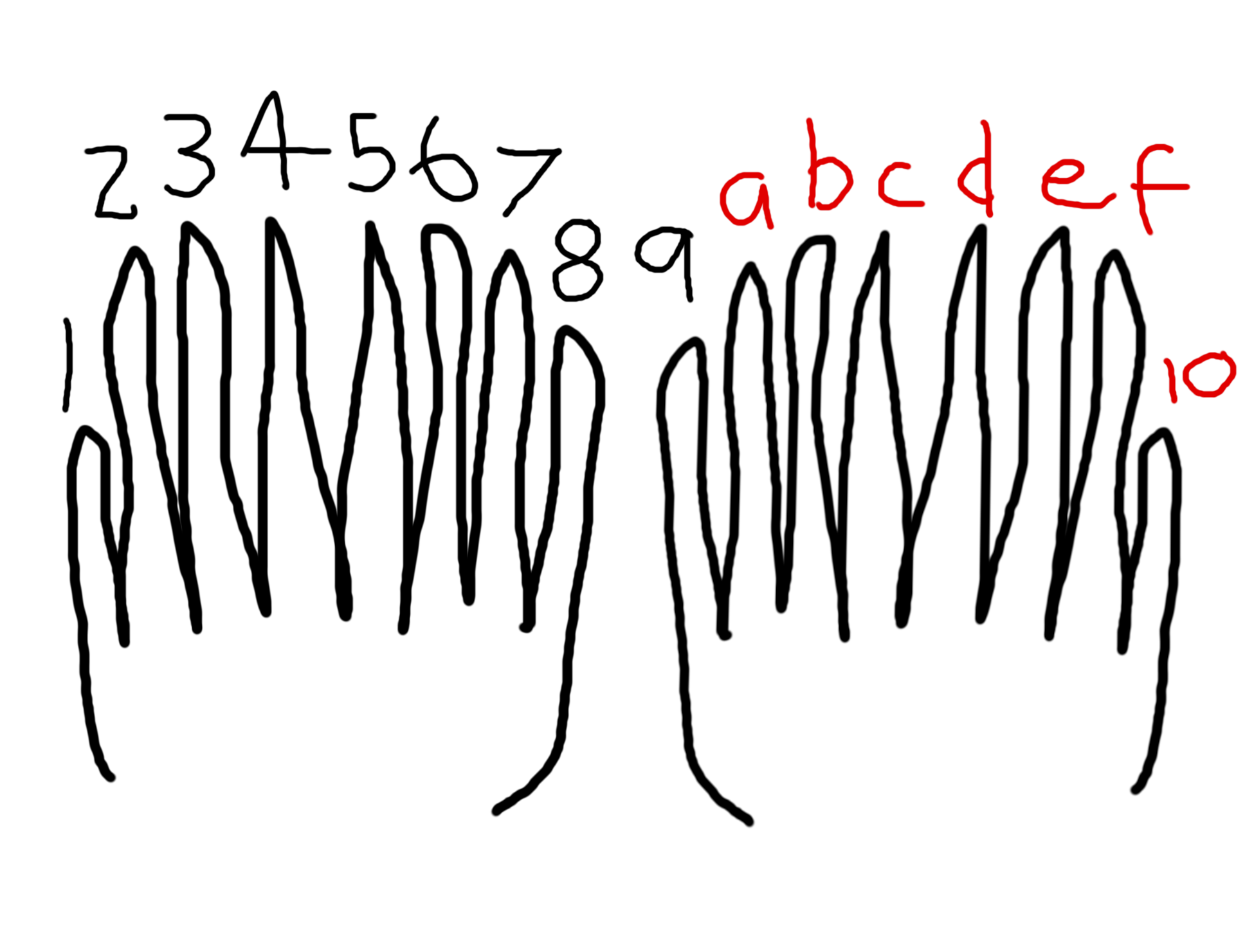
Now, 1610 == 1016. a16 == 1010. Very cool! (The "base" can also be called a "radix".)
This is called hexadecimal (think six + ten == sixteen possible values). One digit is 16 possible values (161), and two digits is 256 possible values (162). This is very useful for representing data in computers. Let's find out why...
Binary
One last alien has arrived... they have two fingers. 0, and 1.
| Binary "bits" | Decimal (human counting) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
There are 10 types of people in the world, those who understand binary and those who don't!
Converting to decimal
Notice how each digit's place represents the value of the radix times the digits value. For example, 102 == 210, or two to the power of one (1*21). 1002 == 1*410, or 22. 10002 == 810, or 1*23.
This holds for all number systems. 100010 has a one in the thousandths place, or 1*103. If we make it 200010, then it's 2*103. We can use this to convert binary numbers to decimal. Let's convert this:
| digit 3 | digit 2 | digit 1 | digit 0 |
|---|---|---|---|
| 1 | 1 | 1 | 0 |
| *23 | *22 | *21 | *20 |
That would be 1*8 (23) plus 1*4 (22) plus 1*2 (21), plus 0*1 (20). 8 + 4 + 2 == 14! So 11102 is 1410. Another!
| #7 | #6 | #5 | #4 | #3 | #2 | #1 | #0 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| *27 | *26 | *25 | *24 | *23 | *22 | *21 | *20 |
That's 128 plus 32 plus 8 plus 4 plus 1, or 17310! You can do this with any number system. Just change the radix :)
Challenge: What is 011111112 in decimal?
The bit
Computers represent everything with 1s or 0s. This is a pretty common concept in pop culture (1s and 0s, very hacker).

Computers need to read values in order to process them. The values are digital (electrical signals). It's much easier to only decipher two states (on and off) than to decipher say, 10. If it was a 5v line, the full 5 volts could be 10, but what's 9? 4.5v? What about 4.3v or 4.7v? 4.75v? Voltage fluctates and there would be many errors in the values being read.
So, 1 corresponds to "on" and 0 corresponds to "off".
The byte
A byte is a collection of bits. How many bits? Well, typically, 8. But there's no reason for it to be 8. It could be 5, or 20, or 48. Long story short, many people decided to use 8 since it was the smallest unit that could represent all the American English letters and symbols. It has eight digits, so it can represent 28 == 256 unique values.
| The byte | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| ... | |||||||
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| ... | |||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Challenge: Computers used to be "32 bit". That means their "register" size (basically, a variable for your CPU) was 32 bits long. What is the max value of a 32-bit register? (Hint: this is why you "can't" have more than 4GB of RAM on a 32-bit computer).
Well... I hate looking at that! Can you instantly spot the difference between 11011110 and 11011100? How much are they different by? Can you imagine trying to confirm you have a number right, and having to read 11010101 01110111 as "one one zero one zero one zero one zero one one one zero one one one"?
Binary (base 2) is the correct choice for computers, but representing it as base 2 is not ideal for humans to read.
Hold on a second... Maybe our eight finger aliens can help! Hexadecimal has sixteen possible values. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, and f. How many values can hexadecimal represent in two digits? 162 == 256.
Eight digits of binary can represent... 28 == 256 values! What about half a byte? Also called a nibble :) 24 == 16 values! That's perfect. We can represent one nibble with one hexadecimal character. We can represent a byte with two hexadecimal characters. Check this out:
| Binary | Hexadecimal | Decimal |
|---|---|---|
| 0 or 0000 | 0 | 0 |
| 1 or 0001 | 1 | 1 |
| 10 or 0010 | 2 | 2 |
| 11 or 0011 | 3 | 3 |
| 100 or 0100 | 4 | 4 |
| 101 or 0101 | 5 | 5 |
| 110 or 0110 | 6 | 6 |
| 111 or 0111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | a | 10 |
| 1011 | b | 11 |
| 1100 | c | 12 |
| 1101 | d | 13 |
| 1110 | e | 14 |
| 1111 | f | 15 |
Instead of 11111111, we can represent it as 0xff. Hexadecimal is special and it gets its own special prefix 0x. (This is because we can't use superscript and subscript likethese in a normal programming language.) If a number starts with 0x, you know it's hexadecimal.
print(10) # prints 10
print(0x10) # ???
The computer always stores our numbers in binary. It stores everything in binary! When you type a letter, a binary set of 1s and 0s is sent to your computer from the keyboard. Then, it's processed by your operating system, and passed to the program you're typing into as a binary value. The program then interprets the binary value and does something with it (like maybe display it as an ASCII-encoded value, for a text editor).
The mapping from binary to hexadecimal is nice and straightforward, and vice versa. Always chunk it into "nibbles", or four bits (a nibble is half a byte...), or one hexadecimal digit.
Converting 1010111101011111 into hexadecimal!
Break into nibbles: 1010 1111 0101 1111 Convert each nibble into hexadecimal based on table: a f 5 f Recombine: 0xaf5f. Done! Much nicer to read!
It's easiest to just memorize the mappings. But if you want, you can go from binary --> decimal --> hexadecimal.
Converting 1010111101011111 into hexadecimal, without using a table!
Break into nibbles: 1010 1111 0101 1111 Convert each nibble into decimal: 8+2 8+4+2+1 4+1 8+4+2+1 10 15 5 15 Convert each decimal value into hex, using our knowledge of the sequence (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f): a f 5 f Recombine: 0xaf5f. Done! Much nicer to read!
Beautiful. Instead of reading 11001010111111101101000000001101, we can read 0xcafed00d. Instead of reading 1001100110111110010101111111000111010011100000100, we can read 0x1337cafe3a704. Much better for us humans.
Another number systems thing: converting from decimal to binary. It's not as easy as the other way around!
Option one: subtract powers of two until the whole number is gone.
Option two: the halfing and checking for odd algorithm. If the number is odd, prepend a 1 to our output and integer divide by 2. If the number is even, prepend a 0 to our output and integer divide by 2.
14 --> even --> 7 --> odd --> 3 --> odd --> 1 --> odd --> 0 --> done 1110! 67 --> odd --> 33 --> odd --> 16 --> even --> 8 --> even --> 4 --> even --> 2 --> even --> 1 --> odd 1000011! Wow! Neat.
Another way to think about that trick is to count all the odds and evens backwards. (We'll do something similar with hexadecimal later, and it makes a bit more sense in that context). Or you can do it the guess and check way :)
Last number systems: converting from hex to decimal and vice versa.
Decimal to hex, convert to decimal the same way we do with binary. Let's convert 0x1f7 to decimal.
| digit 2 | digit 1 | digit 0 | |
|---|---|---|---|
| 1 | f | 7 | |
| *162 | *161 | *160 |
So, 0x1f7 == (1*256) + (0xf*16) + (7*1). That's 256 plus (15*16) plus 7, or 503. All the same rules with converting binary (or any base) to decimal apply here.
How do we convert from hex to decimal? You could convert to binary then use the table to convert nibbles. Or, you could do a modified version of decimal to binary. Instead of dividing by two and using even/odd, we can modulo 16 (to get the remainder) then divide by 16 to go "up" one digit's place.
Challenge: Write a function to convert a decimal number to hexadecimal.
Decimal to hex solution
# Credit to Prof. Hamilton for this solution
def number_into_hex(the_num):
hexits = {
0: '0', 1: '1', 2: '2', 3: '3',
4: '4', 5: '5', 6: '6', 7: '7',
8: '8', 9: '9', 10: 'a', 11: 'b',
12: 'c', 13: 'd', 14: 'e', 15: 'f'
}
result = ''
if the_num == 0:
result = '0'
while the_num != 0:
current_digit = the_num % 16
result = hexits[current_digit] + result
# why don't we use += instead? because that
# would add it to the end, but we want to prepend it
the_num //= 16
return "0x" + result
num = int(input("What number to convert? "))
while num != -1:
print(number_into_hex(num), hex(num))
num = int(input("What number to convert? "))Bitwise operationos
We remember truth tables, that take boolean values. They look like this:
| AND | True | False |
|---|---|---|
| True | TRUE | FALSE |
| False | FALSE | FALSE |
| OR | True | False |
|---|---|---|
| True | TRUE | TRUE |
| False | TRUE | FALSE |
These functions take two "bits" input, True (1) or False (0). And then they produce one bit output. This is a bitwise operation! And there are some more important ones :) Bitwise math is used a LOT in low level computing (like in assembly, which you'll be learning in a future class!).
Let's take AND. If we extend it to act on any number of bits, it would look like this:
1 AND 0 == 0 11 AND 00 == 00 11011 AND 11110 == 11010
Think of it as columns of bits that line up. The Python operator for bitwise AND is &.
>>> bin(0b10 & 0b01)
'0b0' # Python's prefix for binary numbers
# is 0b, but that is not standard
Here are the other ones to know:
Congratulations, you are now a bit twiddling pro :)
Fun: flippy bit
A very fun game to help practice your hexademical and binary number conversions: https://flippybitandtheattackofthehexadecimalsfrombase16.com/